ロストメモリーズ File003で紹介した、「高密度8センチCD-R」。容量を増やすためにトラックピッチを細かくしてそう、と書いたわけですが、その根拠として「なんか二重になってるし、トラックピッチ変わってそうだよね」くらいの説明しかしておらず、だいぶ雑でした。
「妄想で適当なこと書いてんじゃねーよ」くらいのツッコミが来るかと思ってたんですが、エゴサする限りそんなことはなく、受け入れられているようでひとまず安心です。とはいえこれ、特に証拠もなしに書いたわけではありません。実は、簡単な実験でトラックピッチが変化してるのは確認していました。ということで、その方法を紹介します。
なお、やり方だけを知りたい人は、[実験方法]まで読み飛ばしてください。まずは前提の知識として、CD-Rの特徴をザックリ解説
CD-Rにデータを書き込むといっても、目印が何もなければどこに書き込んでいいのかわかりません。この書き込む場所のガイドとして作られているのが、グルーブ(プリグルーブ)です。
グルーブは、中心部から外周部へとグルグルとらせん状に作られている溝のこと。このグルーブに沿ってデータを書き込めば、読み出すときもグルーブを頼ってデータを探せばよく、正しく読み書きできるようになるわけです。
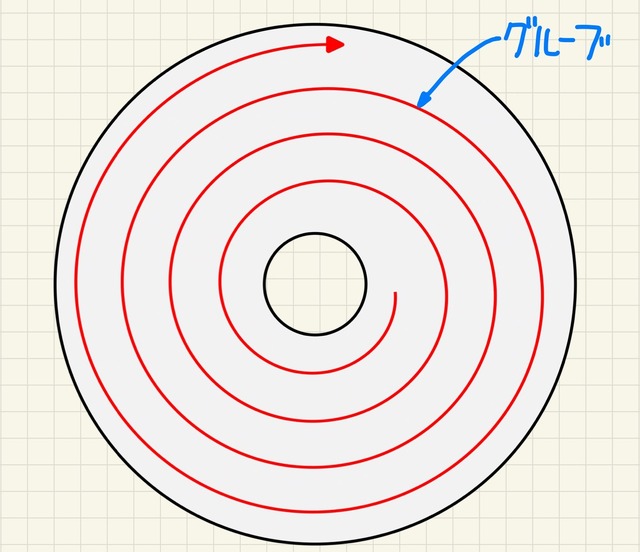
なお、実際のグルーブは一定周期で細かく蛇行しており、回転速度や位置を確認できるようになっています。これをウォブルといいますが、今回は関係ないのでスルーします。
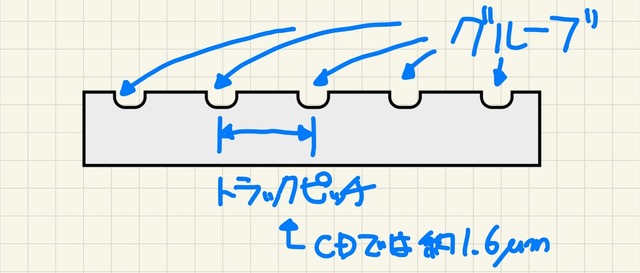
ここでCD-Rの一部を拡大した場合を考えてみましょう。円を描くように緩やかな曲線となっているグルーブですが、グルーブの間隔が十分狭いため、拡大するとほぼ直線とみなせます。つまり、一定間隔ごとに細かな溝をつけた板と考えることができるわけです。
この溝のついた板、どこかで見聞きしたことがないでしょうか。そうです、高校物理などで出てくる回折格子です。
ちなみに、ディスクを回転させるメディアでは情報領域が円弧上に並びますが、この1周ぶんをトラックと呼びます。CD-Rの場合、グルーブとトラックの位置が一致するため、このグルーブの間隔がトラックの間隔、つまりトラックピッチとなります。
一般的なCD-Rのトラックピッチは約1.6μm。つまりCD-Rは、1mmあたり約625本の溝がつけられた回折格子となるわけです。
回折格子にレーザー光を照射すると、干渉で複数の点が現れる
いきなり「回折格子」と言われても、そんなのあったなー……以上に思い出せる人は少ないと思いますので、簡単に説明しておきます。
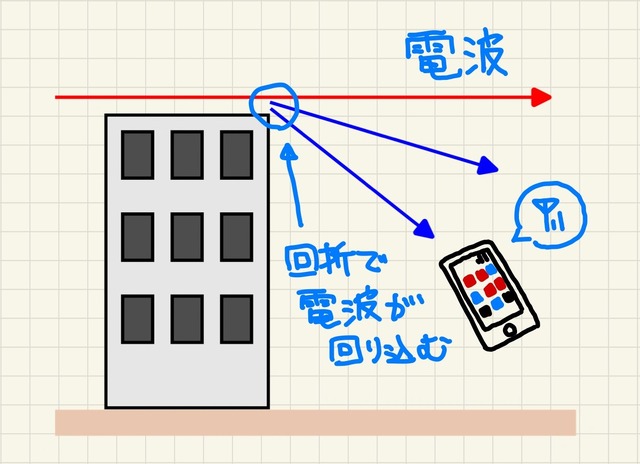
まず「回折」。これは、波が障害物の端にぶつかった場合、その端で遮られるのではなく、そこから放射状に伝わって障害物の裏側にまで回り込む現象のことです。周波数が低いほど、回り込む角度は大きくなります。
身近な例だと携帯電話で使われてる電波がわかりやすいでしょう。以前はソフトバンクが、そして今は楽天モバイルがプラチナバンド(700~900MHz)を要求していますが、これは、2GHz前後の電波よりも繋がりやすいからに他なりません。
繋がりやすいというのは、様々な場所に電波が届くということ。プラチナバンドでは、遠くまで届く、ガラスやコンクリートなどを透過しやすい、建物を回り込んで届く、という特徴がポイントとしてよく挙げられます。
このうち、「建物を回り込んで届く」というのが、回折のことです。プラチナバンドは2GHz前後よりも周波数が低い(波長が長い)ため、障害物の裏側に回り込みやすいわけです。
これは電波の話ですが、光も波の性質を持つため、この回折が起こります。
「回折格子」は溝が等間隔に細かく刻まれていて、いうなれば障害物の端がいくつもズラッと並んでいる状態です。ここに光を当てると、溝の隙間(スリット)で回折した光がいくつも並ぶことになります。
ここで、ある離れた地点から回折格子を見た場合を考えてみましょう。この地点には各スリットで回折した光が届いているのですが、光が通ってくる距離が少しずつ違います。
光が通ってくる距離が違うとどうなるかというと、波の性質により干渉が起こります。干渉とは、同じ波が重なると大きくなり、逆の波が重なると打ち消しあうという現象です。
少し違いますが、綱引きみたいなものと考えるとわかりやすいでしょう。両陣営が交互に引っ張れば中心は大きく動きますが、同時に引っ張れば力が拮抗し、中心はまったく動きません。力を入れる周期が同じであれば、どのくらいタイミングをずらすかで中心部の動く幅が変わってきます。
光の干渉では、綱引きの中心部の動きは明るさの変化となって現れます。タイミングのズレは光が通ってくる距離の違いとなるため、これがちょうど波長の整数倍になると強め合って明るくなり、そこから半波長分ズレると拮抗して暗くなるわけです。
つまり、回折格子を通した光は、観測地点によって明るく見えたり、暗く見えたりするということですね。
試しに、レーザーポインターの光をスクリーンに照射してみましょう。回折格子がない場合はスクリーンに1つの輝点しか映りませんが、回折格子がある場合は回折光が強め合う部分が明るくなり、複数映ります。これが、回折格子による光の干渉です。

ちなみに、回折格子に裏表はなく、どちら側から光を当てても同じ現象が起こります。
[実験方法] スクリーンに映った輝点の距離から、トラックピッチの違いを確認する
ここまでで、CD-Rはトラックピッチで溝を刻まれた回折格子とみなせること、回折格子では各スリットで回折が起こること、回折格子にレーザー光を当てると干渉によってスクリーンに複数の輝点が映る、といったことが理解できたかと思います。
さて本題です。CD-Rが回折格子だということをうまく利用し、高密度8センチCD-Rのトラックピッチが本当に変化しているのか調べてみましょう。
具体的にどうするかというと、レーザーポインターの光をCD-Rへと照射し、反射した回折光をスクリーンに投影。干渉縞となる輝点間の距離を測定します。この距離は回折格子のスリット間隔によって変化するため、ここに変化があれば、トラックピッチが変わっていることが確認できるわけです。
実験装置は、国立大学55工学系学部ホームページで掲載されている、三重大学工学部の「レーザーポインターで測るCDの溝間隔」という記事を参考にしました。


前述の説明では光を回折格子に通過させていましたが、CD-Rを加工するのも大変なので、実験は反射で行っています。光の照射方向が違うだけで、原理的には変わりません。
実際にレーザー光を照射すると、スクリーン上に3つの輝点が並びます。中央は0次回折……つまり、ただの反射なので、ここを基点に1次回折による干渉縞までの距離を測ります。
1次回折は左右どちらにも現れ、基点からの距離も同じになるハズですが、装置の精度やCD面の角度の微妙なズレにより、多少の誤差があります。そのため、2点間の距離を測り、2で割って平均を出しました。

なお、本来なら0次回折となる中央の輝点がレーザー光の照射口と一致するはずですが、まー、ズレますよね。合わせたところで、目視で読み取れる1次回折の距離はまず変わらないため、気にしないことにしました。
今回の実験で使ったのは、8センチの通常CD-R(180MB/21min)、高密度8センチCD-R(300MB/34min)、そしてロストメモリーズの記事内でもちょっと紹介した、GD-ROM(ドリームキャスト用メディア)です。
ちなみに、最初は定規で測ろうと思ってたのですが、装置が動いてしまい現実的ではありませんでした。そのため、1mm方眼紙上に映った輝点を写真に撮り、縦横の長さから計算しています。その結果が以下になります。
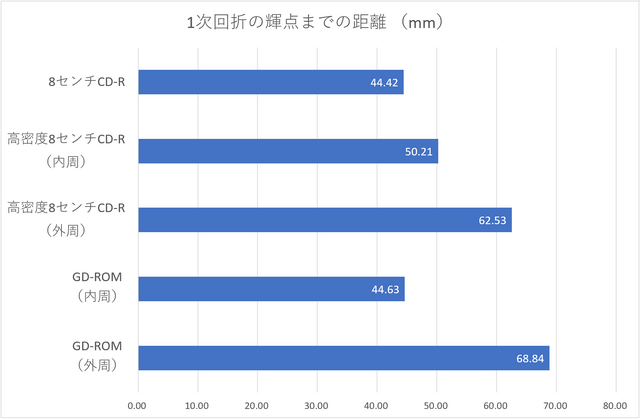
回折格子のスリット間隔(CD-Rではトラックピッチと同意)は、狭くなるほど1次回折の距離が長くなります。高密度8センチCD-Rの結果を見ると、予想通り内外で差が出ており、途中からトラックピッチが変更されていることが確認できました。
ちょっと面白いのは、内周の1次回折距離も、通常のCD-Rより長くなっていること。外周ほど極端ではないものの、ここでも少し容量を稼いでいるようです。
1次回折の距離から、トラックピッチを計算して求める
トラックピッチの変化を確認するだけならここで終わりですが、実際どのくらいのトラックピッチで作られているのか、気になりますよね。
1次回折の距離は、照射する光の波長、回折格子のスリット間隔、スクリーンまでの距離によって計算できます。裏を返せば、1次回折の距離がわかっていれば、計算によって回折格子のスリット間隔……つまり、CD-Rのトラックピッチを求められるわけです。
なお、ここまで理解しやすいよう数式を避けて説明してきましたが、さすがにトラックピッチを求めるには計算が必要となるため、ここからは遠慮しないことにします。
さて、先の回折格子の説明で書いたことを要約すると、
観測地点には、各スリットごとに回折した光が多数届いている
それぞれの回折光は、通ってくる距離が少しずつ違う
この距離の差が波長の整数倍だと明るくなる
となります。
まず求めるのは、回折光が通ってくる距離の差がどのくらいなのか、ということ。これは三角関数で簡単に求めることができ、スリットの間隔をd(回折格子では、このdを格子定数といいます)、観測地点の方角がθとすると、1つスリットがずれるたびにd sinθぶん、距離が長くなるわけです。
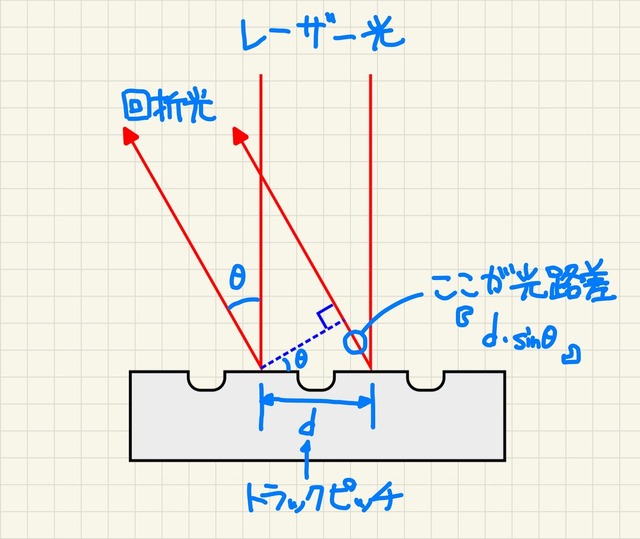
レーザーポインターの波長をλとすると、干渉条件は波長の整数倍となるため、
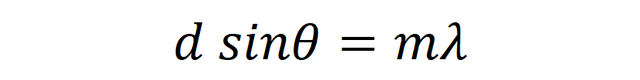
と表せます。
トラックピッチ(スリット間隔)dを求めるのですから、
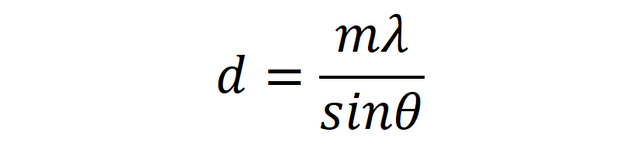
を計算すればいいことになります。
ところで、sinθを求めるには角度θを測る必要がありますが、分度器などを使った手作業で行うのは現実的ではありません。ここで、実験装置にレーザー光を照射した状態を概略図にしたものを見てみましょう。
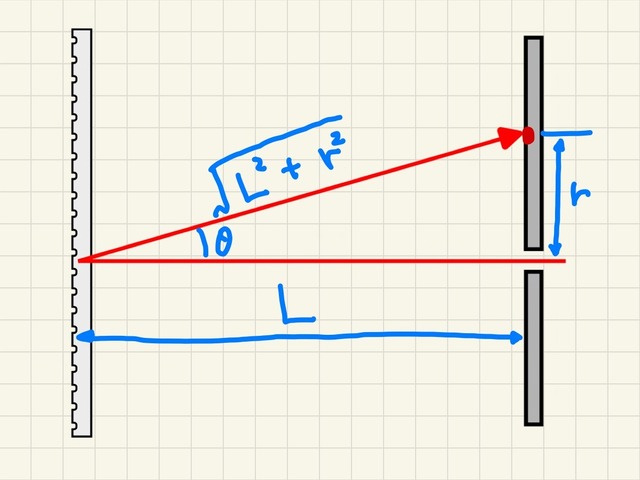
θは横L、縦rとする直角三角形の角となるため、sinθをLとrを用いて数式に直すと、
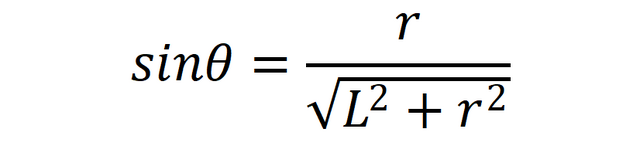
となります。これをdの式に代入します。
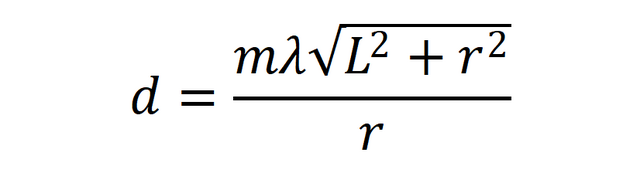
今回の実験では1次回折を利用するのでmが1。使用したレーザーポインターの波長λは製品に650nmと書かれていたので、これを採用します。スクリーンとCD-R面の距離Lを100mmとして実験を行っているので、これも代入して計算するとトラックピッチが求まります。
ということで、その結果がこちらです。
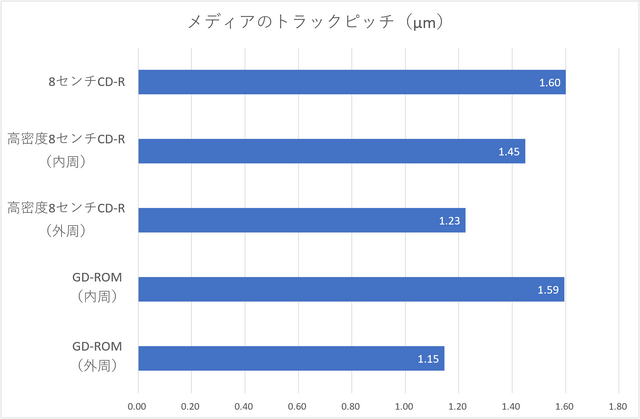
簡単な実験でも、未知のトラックピッチが求められる
高密度8センチCD-Rは思っていた以上にトラックピッチが細かく、よくこれが普通のCD-R対応ドライブで読み書きできるものだと、改めて驚きました。
トラックピッチを細かくしたCD規格にDDCDがありますが、従来CDとの互換性はなく、メディアもドライブも専用品が必要となるため、普及しませんでした。このとき、まともにDDCDという規格を作るのではなく、「規格外でも使えるから作る」という姿勢で1GBくらいの「高密度12センチCD-R」を出していたら、もう少しCD-Rの寿命が延びていたかもしれないですね。
といっても、DVD±Rは4.7GBと数倍容量が大きいので、延びても本当にちょっとだけだと思いますけど。
高密度8センチCD-Rがなぜ内周、外周で異なるトラックピッチを採用していたのかの謎は残りますが、ロストメモリーズで断言できなかった部分を、実験で補足できたのはよかったです。
この実験はかなり簡単なので、物理に興味をもってもらう入り口として、なかなか楽しめるのではないでしょうか。DVDやBD、HD DVD、MO、MD、PD、iD PHOTOなど、身近な光学メディアでトラックピッチを測定してみると面白いかもしれません。
おまけ
高密度8センチCD-Rのトラックピッチが変わる境界部分で、回折がどうなるのか気になったため、試してみた結果がこちら。

レーザー光の径がトラックピッチよりだいぶ大きいので、トラックピッチの変化が全部映されていると考えられます。干渉が点ではなく線になるということは、緩やかにトラックピッチが変化しているという可能性が高そうです。
参考文献:
「メディア編 第10回 データを光で記録する」, コンピュータ講座応用編, FUJITSUファミリ会
「回折格子(グレーティング)の解説」, 島津製作所
「レーザーポインターで測るCDの溝間隔」, 国立大学55工学系学部ホームページ













